Lojistik Regresyon

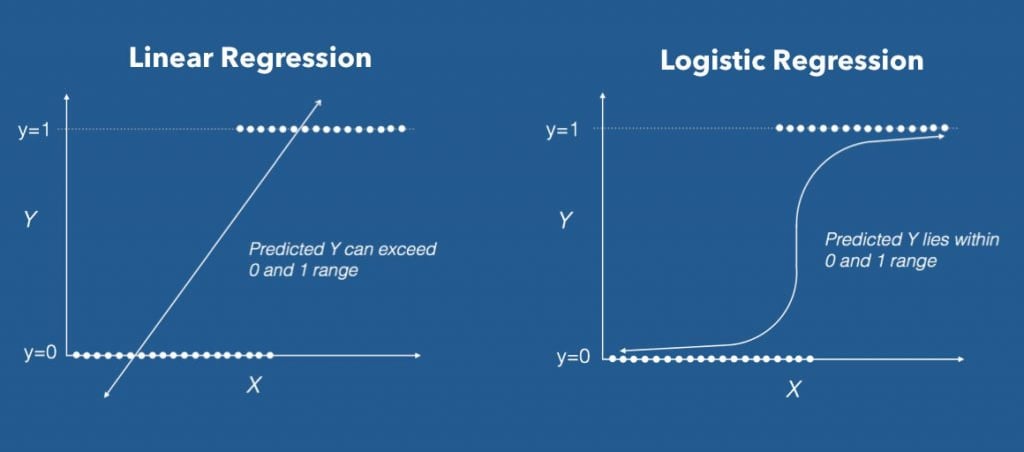
Lojistik regresyon, özellikle sınıflandırma problemlerinde kullanılan bir istatistiksel modelleme yöntemidir. Bağımlı değişkenin kategorik olduğu durumlarda, özellikle ikili (binary) sonuçlar içeren veri setlerinde yaygın olarak tercih edilir. Örneğin, bir hastanın hasta olup olmadığını, bir e-postanın spam olup olmadığını ya da bir müşterinin ürünü alıp almayacağını tahmin etmek gibi durumlar lojistik regresyonla analiz edilebilir.

Lojistik regresyonun amacı, iki yönlü karakteristiği (bağımlı değişken = yanıt veya sonuç değişkeni) ile ilgili bir dizi bağımsız (öngörücü veya açıklayıcı) değişken arasındaki ilişkiyi tanımlamak için en uygun (henüz biyolojik olarak makul) modeli bulmaktır. Lojistik regresyon, ilgi karakteristiklerinin varlığının olasılığını logit dönüşümünü tahmin etmek için bir formülün katsayılarını (standart hatalarını ve önem seviyelerini) üretir.

UYGULAMA ALANLARI

Lojistik regresyon, birçok alanda yaygın olarak kullanılmaktadır:

• Sağlık: Bir hastanın belirli bir hastalığı taşıyıp taşımadığını tahmin etmek.

• Pazarlama: Bir müşterinin kampanyaya yanıt verip vermeyeceğini öngörmek.

• Finans: Bir kişinin kredi geri ödemesini yapıp yapamayacağını tahmin etmek.

• Sosyal Bilimler: Anket sonuçlarına göre bireylerin davranışlarını modellemek.

• Spam Filtreleme: Bir e-postanın spam olup olmadığını sınıflandırma.

Lojistik Regresyon, diğer gelişmiş sınıflandırma algoritmalarının (SVM, Karar Ağaçları, Sinir Ağları) temelini anlamak için de harika bir başlangıç noktasıdır.

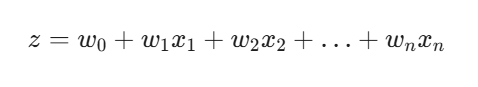
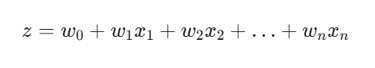
Burada:

• z: Doğrusal modelin çıktısı

• w0: Kesme noktası (Bias)

• wi: Her bir özelliğin ağırlığı (katsayısı)

• xi: Giriş özellikleri (features)

2. Sigmoid Fonksiyonu (Lojistik Fonksiyon)

Doğrusal modelin çıktısı olan z, - ∞ile +∞ arasında herhangi bir değer alabilir. Sınıflandırma için bu değeri bir olasılığa çevirmemiz gerekir. İşte bu noktada Sigmoid Fonksiyonu ( h(z) ) devreye girer.

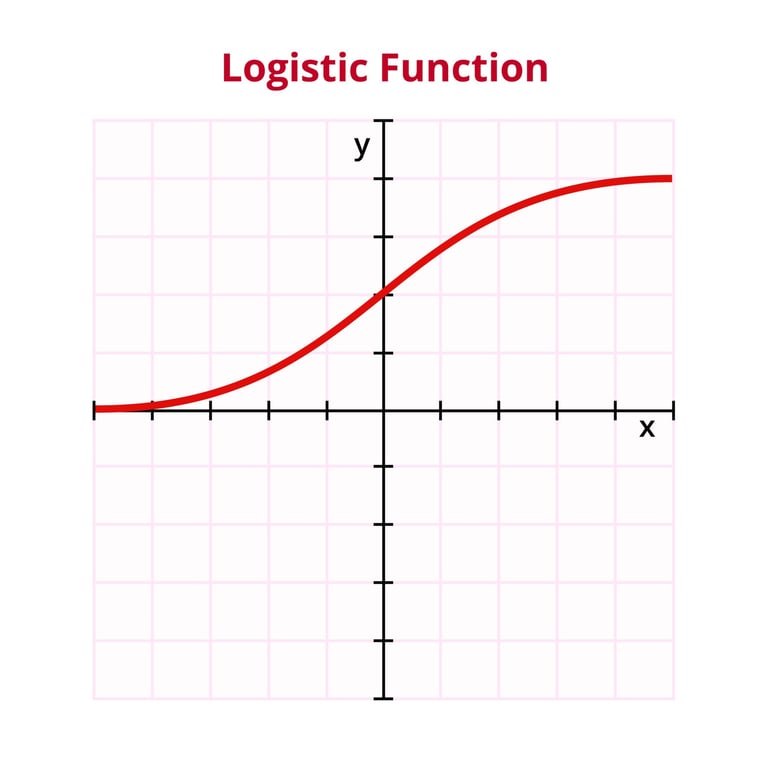
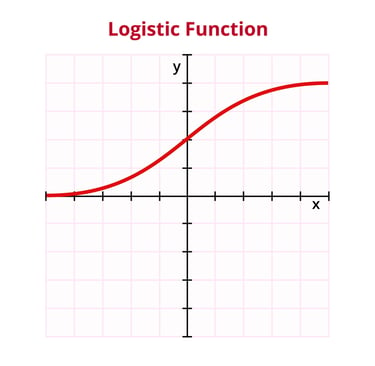
Sigmoid fonksiyonu, z değerini 0 ile 1 arasına sıkıştırır ve bize pozitif sınıfa ait olma olasılığını verir:

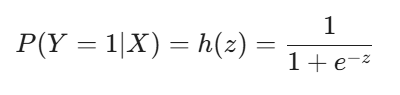
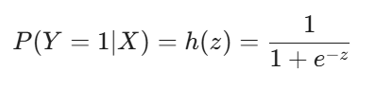
Bu olasılık değeri, tahmin edilen sınıfı belirlemek için bir eşikle (genellikle 0.5) karşılaştırılır:

• Eğer P(Y=1|X) ≥ 0,5 ise, tahmin edilen sınıf 1'dir.

• Eğer P(Y=1|X) < 0,5 ise, tahmin edilen sınıf 0'dır.

Model Eğitimi (Maliyet Fonksiyonu)

Lojistik Regresyon'da, modelin ağırlıklarını (wi) optimize etmek için Maksimum Olabilirlik Tahmini (Maximum Likelihood Estimation - MLE) kullanılır. Bu, verilen ağırlıklarla gözlemlenen veri kümesini elde etme olasılığını maksimize etmeye eşdeğerdir.

Bunu yapmak için, genellikle Çapraz Entropi (Cross-Entropy) veya Log Kaybı (Log Loss) olarak bilinen bir maliyet fonksiyonu kullanılır. Bu fonksiyon, tahmin edilen olasılık ile gerçek etiket arasındaki farkı cezalandırır:

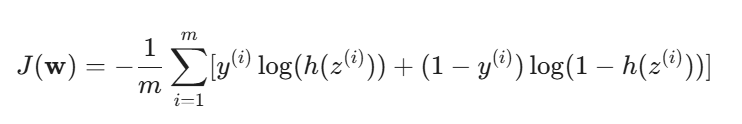
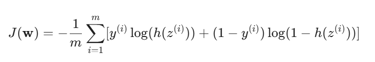
• yi: Gerçek etiket (0 veya 1).

• h(z^i): Tahmin edilen olasılık.

• m: Eğitim örneklerinin sayısı.

Model, bu maliyet fonksiyonunu Gradyan İnişi (Gradient Descent) gibi optimizasyon algoritmaları kullanarak minimize edecek ağırlık (wi) değerlerini öğrenir.

Nasıl Çalışır

Lojistik Regresyon'un çalışma mekanizması iki ana adımdan oluşur:

1. Doğrusal Modelin Oluşturulması

Öncelikle, tıpkı Doğrusal Regresyon'da olduğu gibi, girdi özelliklerinin ( x1, x2, ... , xn ) ağırlıklı toplamı hesaplanır:

Avantajları ve Dezanatajları

Avantajları:

• Basit ve Hızlı: Uygulaması ve eğitilmesi oldukça kolay ve hızlıdır.

• Yorumlanabilirlik: Modelin katsayıları (ağırlıkları) kolayca yorumlanabilir. Bir özelliğin katsayısı, o özelliğin çıktı olasılığı üzerindeki etkisini gösterir.

• Olasılık Çıktısı: Sonuç olarak sadece bir sınıf etiketi değil, aynı zamanda bu sınıfa ait olma olasılığını da verir.

Dezavantajları:

• Doğrusallık Varsayımı: Özellikler ve çıktı değişkeni arasında doğrusal bir ilişki olduğunu varsayar (Sigmoid'den önceki z kısmı). Karmaşık, doğrusal olmayan ilişkileri modellemede zorlanabilir.

• Aşırı Uçlara Duyarlılık: Tıpkı Doğrusal Regresyon gibi, aşırı uç (outlier) değerlere karşı hassastır.

• Özellik Ölçeklemesi: Farklı ölçeklere sahip özellikler, modelin performansını olumsuz etkileyebilir. Bu nedenle özelliklerin ölçeklenmesi (normalizasyon) genellikle önerilir.

TEORİK TEMELLERİ

Lojistik regresyon, lineer regresyonun bir türevi gibi düşünülebilir, ancak önemli bir farkı vardır: Lineer regresyon sonuçları sürekli sayılarla ifade ederken, lojistik regresyon sonuçları 0 ile 1 arasında bir olasılık değeri üretir. Bu olasılık değeri, belirli bir koşulun gerçekleşme ihtimalini gösterir. Model, bu olasılığı tahmin etmek için "lojistik (sigmoid) fonksiyon" adı verilen S şeklinde bir fonksiyon kullanır.

Katsayıların Yorumlanabilirliği (Odds Oranı)

Lojistik Regresyon'un en güçlü yanlarından biri, her bir özellik için öğrenilen ağırlıkların ($w_i$) bize bu özelliğin olasılık üzerindeki etkisini net bir şekilde söylemesidir.

Doğrusal regresyonda katsayılar doğrudan $Y$ üzerindeki etkiyi gösterirken, Lojistik Regresyon'da katsayılar Odds Oranı (Odds Ratio) üzerinden yorumlanır.

Odds Nedir?

Odds (Oran), bir olayın gerçekleşme olasılığının ($P$), gerçekleşmeme olasılığına ($1-P$) bölünmesiyle bulunur:

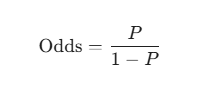
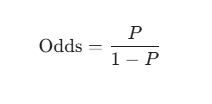
Odds Oranı ve Katsayılar (wi)

Bir özelliğin katsayısı ($w_i$) ne kadar büyük ve pozitifse, o özellik pozitif sınıfın (1) olasılığını o kadar artırır. Bu ilişkiyi anlamak için $w_i$'nin üstelini (e^wi) alırız.

e^wi değeri, ilgili xi özelliğinin bir birim artmasının, Odds Oranını kaç kat artırdığını gösterir.

Model Uyum İstatistikleri (Goodness of Fit)

Bu istatistikler, modelin gözlemlenen verilere ne kadar iyi uyduğunu ölçer.

1. Olabilirlik Oranı Testi (Likelihood Ratio Test)

• Amaç: Modelin, sadece kesme terimini içeren (null) modele göre anlamlı bir gelişme sağlayıp sağlamadığını test eder.

• İstatistik: X^2 (Ki-kare) dağılımına sahip olan Olabilirlik Oranı X^2 İstatistiği kullanılır.

• P-Değeri: Eğer X^2 istatistiğinin p-değeri (genellikle 0.05'ten) küçükse, modelin genel olarak anlamlı olduğu ve yordayıcıların modele katkıda bulunduğu sonucuna varılır.

2. Pseudo R^2 Metrikleri

Doğrusal regresyondaki R^2 (Açıklanan Varyans Oranı) metriğinin bir karşılığıdır, ancak Lojistik Regresyon'da tam olarak aynı şekilde yorumlanmaz. Modelin, null modele kıyasla açıklamadaki iyileşmesini gösterir.

• Cox ve Snell R^2:

• Nagelkerke R^2: En sık kullanılan Pseudo R^2 metriğidir ve maksimum değeri 1 olacak şekilde normalize edilmiştir. Yüksek bir değer (0.20 ve üzeri kabul edilebilir sayılabilir) daha iyi bir uyum anlamına gelir.

3. Hosmer-Lemeshow Testi

• Amaç: Modelin kalibrasyonunu, yani tahmin edilen olasılıkların gerçekleşen sonuçlara ne kadar uyduğunu kontrol etmek için kullanılan bir uyum testidir.

• İstatistik: Gözlenen ve beklenen olay sayıları arasındaki farkları özetleyen bir X^2 istatistiği hesaplanır.

• Yorum: Büyük bir p-değeri (genellikle 0.05'ten büyük) iyi bir uyum gösterir, çünkü null hipotez (modelin iyi bir uyuma sahip olduğu) reddedilemez.