Karar Ağacı / CART

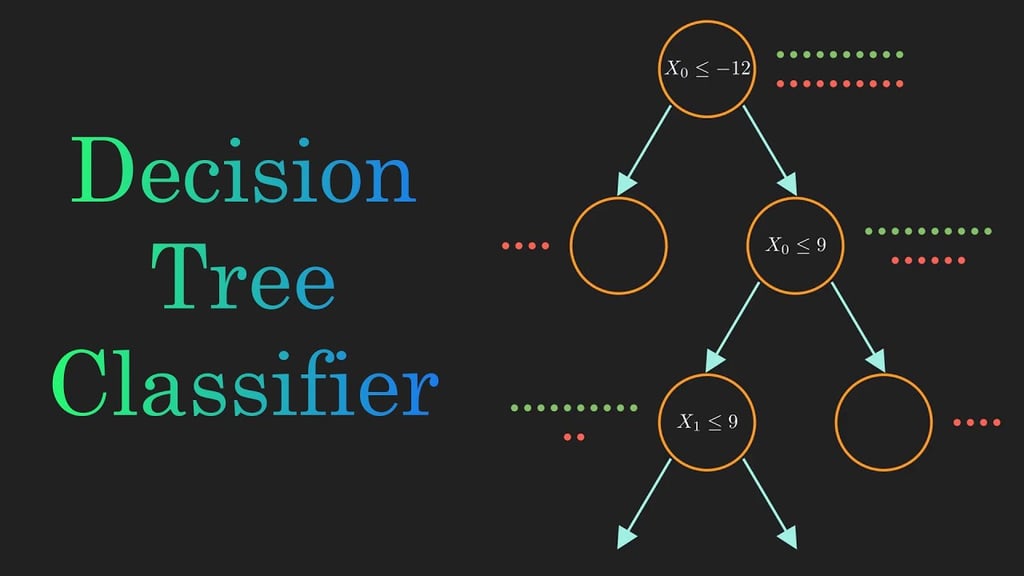
Karar ağacı, risklerin, kazançların ve hedeflerin anlaşılmasına yardımcı olan bir teknik türüdür. Aynı zamanda birçok önemli yatırım sahalarında uygulanabilen, birbiriyle bağlantılı şans olaylarıyla ilgili olarak çıkan çeşitli karar noktalarını incelemek için kullanılan bir karar destek aracıdır. Yalnızca koşullu kontrol ifadeleri içeren bir algoritmayı görüntülemenin bir yoludur.

Karar ağacı, bir hedefe ulaşma olasılığı en yüksek olan stratejiyi belirlemeye yardımcı olmak için kullanılan bir yöntemdir. Özellikle karar analizinde olmak üzere karmaşık sorunların araştırmasında yaygın olarak kullanılmaktadır.

Karar ağacının avantajları:

• Anlaması ve yorumlaması basit. İnsanlar kısa bir açıklamadan sonra karar ağacı modellerini anlayabilecektir.

• Bir durumu (alternatifleri, olasılıkları ve maliyetleri) ve sonuç tercihlerini tanımlayan uzmanlara dayalı olarak önemli ön görüler oluşturulabilmektedir.

• Farklı senaryolar için en kötü, en iyi ve beklenen değerlerin belirlenmesine yardımcı olmaktadır.

• Diğer karar teknikleriyle birleştirilebilmektedir.

Karar ağacının dezavantajları:

• Kararsızdırlar, yani verilerdeki küçük bir değişikliğin, en iyi durumdaki karar ağacının yapısında büyük bir değişikliğe yol açabileceği anlamına gelmektedir.

• Genellikle hatalıdırlar. Diğer birçok tahmin algoritmaları benzer verilerle daha iyi performans gösterir. Bu, tek bir karar ağacını rastgele orman ile değiştirerek düzeltilebilir, ancak rastgele ormanın tek bir karar ağacı kadar yorumlanması kolay değildir.

• Farklı sayıda seviyeye sahip kategorik değişkenler içeren veriler için, karar ağaçlarındaki bilgi kazanımı, daha fazla seviyeye sahip öznitelikler lehine önyargılıdır.

• Hesaplamalar çok karmaşık hale gelebilir, özellikle de birçok değer belirsizse veya birçok sonuç ile bağlantılıysa.

1. Sınıflandırma Metrikleri (Homojenliği Ölçmek)

Sınıflandırma ağaçlarında (Classification Trees), bir düğümdeki verilerin ne kadar "karışık" (saf değil) olduğunu ölçmek için iki ana metrik kullanılır:

A. Gini Kirliliği (Gini Impurity)

Gini kirliliği, rastgele seçilen bir öğenin yanlış sınıflandırılma olasılığını ölçer. Amacımız, Gini kirliliğini en aza indiren bölünmeyi bulmaktır.

Bir düğümdeki j sınıfının oranı pj olmak üzere, Gini Kirliliği IG şu şekilde hesaplanır:

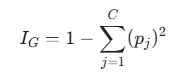
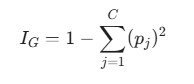
• C: Toplam sınıf sayısı.

• Amaç: Bir düğüm bölündükten sonra, alt düğümlerin $I_G$ değerlerinin ağırlıklı ortalamasını minimize etmektir. $I_G$ sıfıra (0) ne kadar yakınsa, düğüm o kadar saftır (homojendir).

B. Entropi ve Bilgi Kazancı (Entropy and Information Gain)

Entropi, bir sistemdeki rastgelelik veya düzensizlik (bilgisizlik) ölçüsüdür. Entropi ne kadar yüksekse, verideki karışıklık o kadar fazladır.

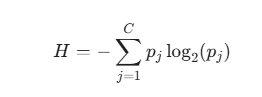
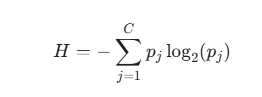
Bilgi Kazancı (Information Gain - IG), bir bölünme sonucunda Entropi'deki azalmayı ölçer. Algoritma, en yüksek Bilgi Kazancını (yani Entropi'deki en büyük azalmayı) sağlayan özelliği ve bölünme noktasını seçer.

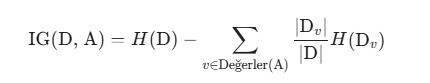
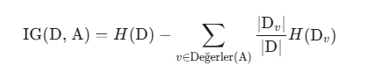
2. Regresyon Metrikleri

Regresyon ağaçlarında (Regression Trees), amaç bir sınıf etiketi tahmin etmek yerine sürekli bir değer tahmin etmek olduğundan, homojenlik (saflık), tahmini değerin ne kadar iyi temsil edildiği ile ölçülür.

Temel olarak kullanılan metrik Ortalama Kare Hata (Mean Squared Error - MSE) veya varyans azalmasıdır. Algoritma, alt düğümlerdeki varyansı en aza indirecek bölünmeyi seçer.

Bir düğümün MSE'si, o düğümdeki örneklerin ortalama değere olan sapmalarının karesiyle hesaplanır. Bölünme, MSE'yi en çok azaltan özellik ve eşik değerine göre yapılır.

3. Aşırı Uyum ve Budama (Overfitting and Pruning)

Karar Ağaçları'nın en büyük akademik zorluğu, eğitim verisine aşırı uyum (overfitting) eğilimidir. Ağaç, her yaprak düğümünde yalnızca tek bir örneği bırakacak kadar derine inerse, eğitim verisini mükemmel ezberler ancak yeni, görünmeyen verilerde kötü performans gösterir.

Bu durumu önlemek için Budama (Pruning) teknikleri kullanılır:

• Ön Budama (Pre-pruning): Ağacın büyümesini, bir düğümdeki örnek sayısı belirli bir eşiğin altına düştüğünde veya bölünmeden sonraki bilgi kazancı çok düşük olduğunda durdurur.

• Art Budama (Post-pruning): Tamamen büyümüş bir ağacı oluşturduktan sonra, genelleme yeteneğini artıran düğümleri keser. Buna, Maliyet Karmaşıklığı Budaması (Cost-Complexity Pruning) örnek verilebilir.

Bu matematiksel ve istatistiksel temeller, Karar Ağaçları'nın neden güçlü bir temel algoritma olduğunu gösterir.