Çoklu Doğrusal Regresyon Analizi

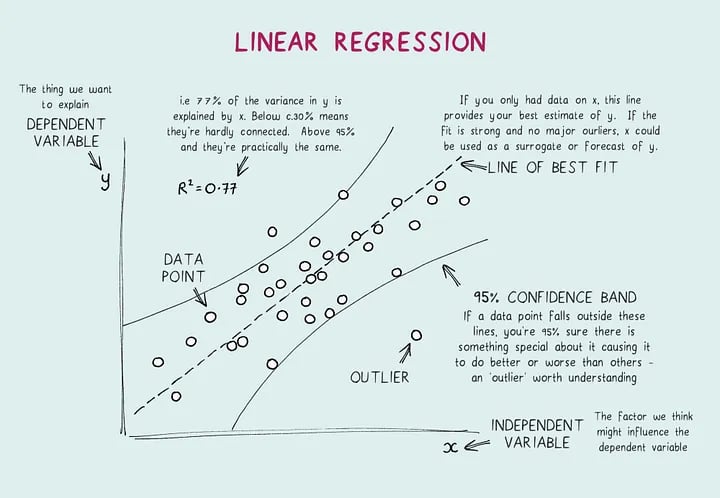
Gönderi içeriğim

Çoklu doğrusal regresyon, bir bağımlı değişkenin (y) birden fazla bağımsız değişkene (x1, x2, x3, ...) olan doğrusal ilişkisini inceleyen istatistiksel bir tekniktir. Basit doğrusal regresyonda sadece bir bağımsız değişken varken, çoklu doğrusal regresyonda birden fazla değişken vardır.

Temel Denklem:

Y = β₀ + β₁X₁ + β₂X₂ + ... + βₙXₙ + ε

• Y: Bağımlı değişken (tahmin edilen değer)

• X₁, X₂, ..., Xₙ: Bağımsız değişkenler

• β₀: Sabit terim (intercept)

• β₁, β₂, ..., βₙ: Katsayılar (her bir X'in Y üzerindeki etkisi)

• ε: Hata terimi (modelin açıklayamadığı kısım)

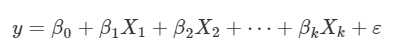
(1.1)

1. En Küçük Kareler Kestirimi

𝛽0 , 𝛽1 , 𝛽2,…, 𝛽𝑘 parametreleri bilinmeyenlerdir ve örneklem verileri üzerinden kestirimler gerekir. (𝑦1, 𝑥11, 𝑥12, … , 𝑥1𝑘 ), … , (𝑦𝑛, 𝑥𝑛1, 𝑥𝑛2, … , 𝑥𝑛𝑘) olmak üzere n sayıda ve k bağımsız değişkenden oluşan veri kümesi olduğu varsayılır.

1.1. Regresyon Katsayılarının En Küçük Kareler Kestirimi

𝑦𝑖 , 𝛽1 , 𝛽2,…, 𝛽𝑘 gözlemleri ile regresyon doğrusu arasındaki farkın en küçük olacak şekilde kestirilir. Denklem (1.1)’deki regresyon katsayılarının kestirimi için kullanılır. n>k gözlemin olduğunu varsayılarak aşağıdaki denklem yazılır.

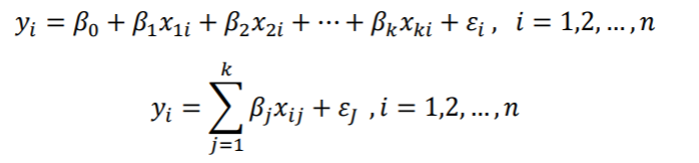
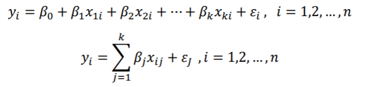
(1.2)

En küçük kareler fonksiyonu aşağıdaki gibidir:

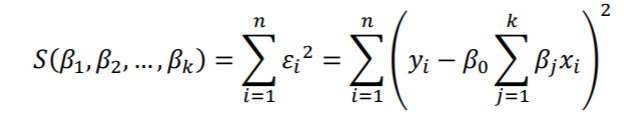
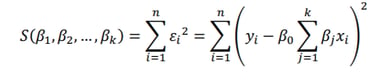
(1.3)

Denklem (1.2) 𝛽0 , 𝛽1 , 𝛽2 ,…, 𝛽𝑘 göre ayrı ayrı türevi alınıp sıfıra eşitlenirse,

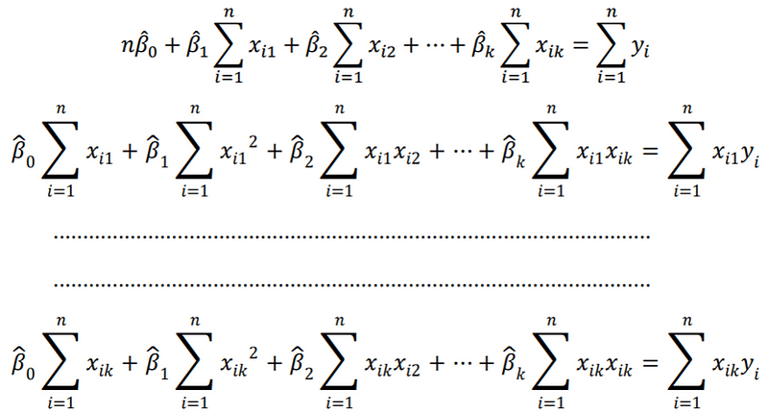
(1.4)

Denklemini verir. Bu denklemler en küçük kareler normal denklemleri olarak adlandırılır. Normal denklemlerinin çözümü 𝛽0 , 𝛽1 , 𝛽2 ,…, 𝛽𝑘 en küçük kareler kestiricilerini verecektir.

Çoklu regresyon modelleriyle ilgilenirken onları matris içinde ifade etmek daha uygundur. Verilerin ve sonuçların daha kısa ve öz bir biçimde ortaya çıkmasınısağlar Denklem(1.2)’da verilen modelin matris gösterimi,

𝑦 = 𝑋𝛽 + 𝜀 biçimindedir. Burada ki, matrisler aşağıdaki gibidir;

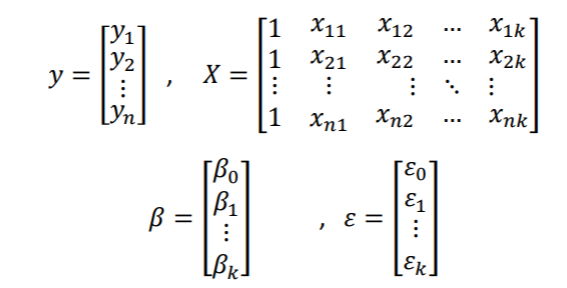
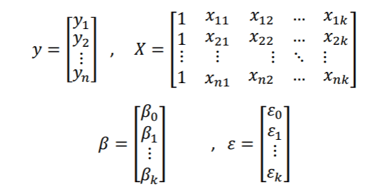
(1.5)

y:Gözlemler vektörü

X:Bağımsız değişkenler matrisi

𝛽:Regeresyon Katsayıları vektörü

𝜀:Rasgele hatalar vektörü

Aşağıda verilen 𝑆(𝛽) fonsiyonunu minimize ederek 𝛽̂ en küçük kareler kestiricileri vektörünü elde ederiz:

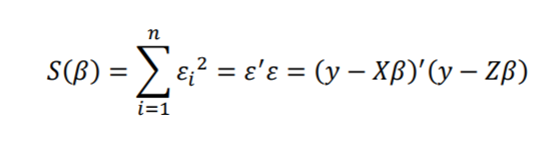
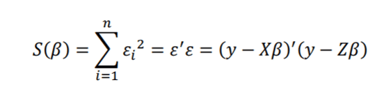
(1.6)

𝑆(𝛽) aşağıdaki gibi elde edilir:

(1.7)

Denklem (1.7) 𝛽’ya göre türevi alınıp basitleştirilirse:

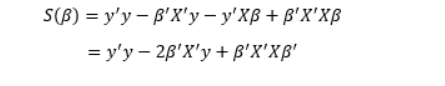
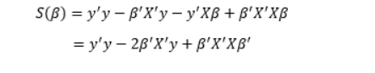
(1.8)

Denklem(1.8)’ün matris gösterimi aşağıdaki gibidir

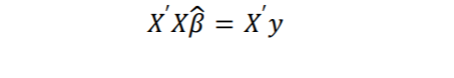
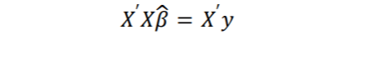
(1.9)

Denklem(1.9)’ün matris gösterimi aşağıdaki gibidir.

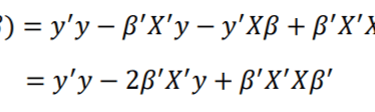
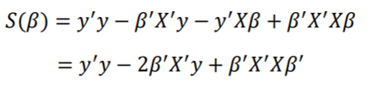
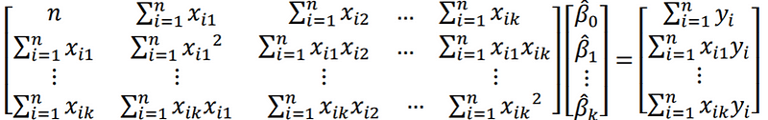
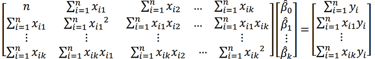
(1.10)

Denklemi(1.10) çözmek için her iki tarafı (X’X)^-1 ile çarpılır. 𝛽’nın en küçük kareler kestiricisi bulunur.

(1.11)

1.2. 𝝈² ’nin kestirimi

İdeal olarak bu kestirimin kurulan modelin yeterliliğine bağlı olmaması tercih edilir. Bu ise yanlızca x’in en az bir değeri için y üzerinde farklı gözlemler olduğunda ya da 𝜎²’ye ilişkin önceliğinden elde edilmiş bilgi bulunduğunda mümkün olmalıdır. Bu yaklaşım kullanılamadığında 𝜎², artık veya hata kareler toplamından elde edilir.

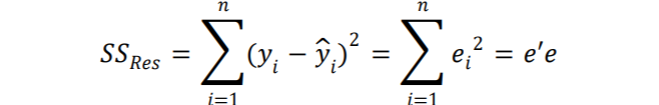
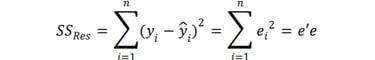
(1.12)

𝑒 = 𝑦 − 𝑋𝛽̂ yerine konulmasıyla aşağıdaki ifade elde edilir

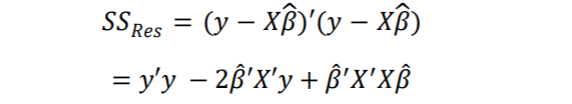
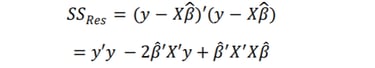
(1.13)

Denklem (1.12)’ten son denklem aşağıdaki gibi olur.

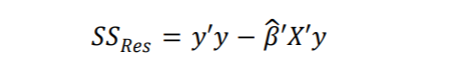
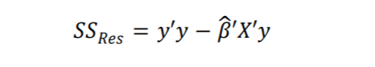
(1.14)

Artık kareler toplamını n-p serbestlik derece sine sahiptir. SSRes’in beklenen değeri E(SSRes)=(n-p)𝜎² olduğu göstermektedir; dolayısı ile 𝜎²’nin yansız bir kestiricisi aşağıdaki gibidir:

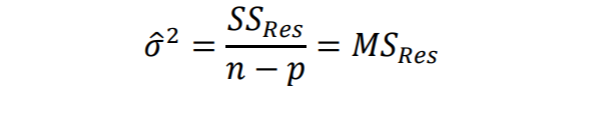
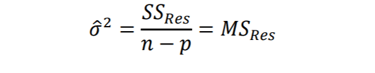
(1.15)

1.3. Dummy Değişken

2 ve daha fazla kategorisi olan bir değişkeni 1 ve 0 şeklinde kodladığımızda aslında tek kategoriye indirmiş oluyoruz. Örneğin erkek=0 kadın=1 olarak kodlandığında değişkeni kadın olmak ya da olmamak şeklinde yorumlayarak regresyon analizi yapılır. Burada yaptığımız bir grubu referans grubu alıp sadece diğer grubun verileri ile analiz yapıp daha sonra elde edilen regresyon katsayısını da analize katılan grup üzerinden yorumlamaktır.

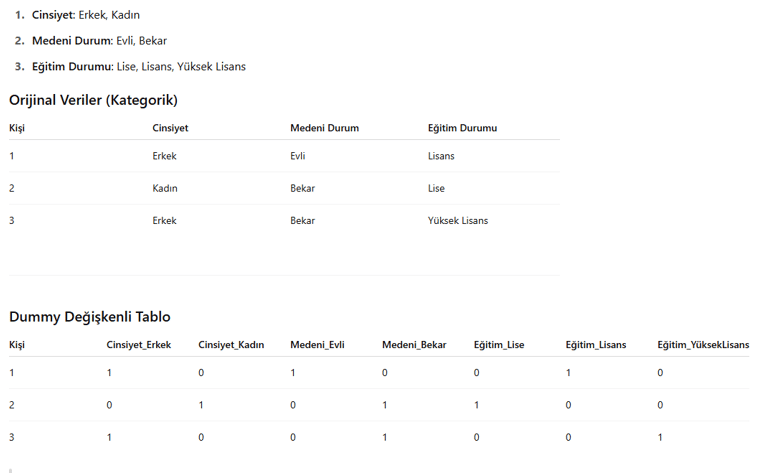
Not: Gerçek regresyon modellerinde "dummy trap" yani çoklu doğrusal bağlantıyı önlemek için genelde her kategoriden bir tanesi silinir. Örneğin:

• Cinsiyet_Kadın, Medeni_Bekar, Eğitim_Lise gibi değişkenler çıkarılır, ve onlar baz (referans) kategori olarak kabul edilir.